This course can also be taken for academic credit as ECEA 5611, part of CU Boulder’s Master of Science in Electrical Engineering degree.
Theory of Angular Momentum
Heat up your career with 40% off top courses from Google, Adobe, and more. Save today.
Theory of Angular Momentum
This course is part of Quantum Mechanics for Engineers Specialization
Instructor: Wounjhang Park
5,990 already enrolled
Included with 
Gain insight into a topic and learn the fundamentals.
4.0
(20 reviews)
Intermediate level
Recommended experience
Flexible schedule
Approx. 12 hours
Learn at your own pace
Build toward a degree
What you'll learn
Specify the quantum states of the electron in a hydrogen atom.
Describe spin states quantum mechanically.
Solve eigenvalue equations of angular momentum operators.
Add general angular momenta.
Skills you'll gain
Details to know
Shareable certificate
Add to your LinkedIn profile
Assessments
3 assignments
Taught in English
See how employees at top companies are mastering in-demand skills
Build your subject-matter expertise
This course is part of the Quantum Mechanics for Engineers Specialization
When you enroll in this course, you'll also be enrolled in this Specialization.
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate
There are 3 modules in this course
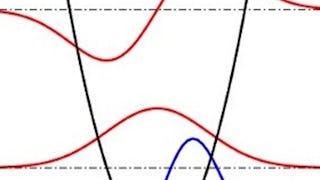
In this module we will introduce the course on the theory of angular momentum and then introduce the quantum mechanical definition of orbital momentum. We will then use the spherical harmonics to express the orbital angular momentum eigenstates and use them to describe the hydrogen atom states.
What's included
5 videos4 readings1 assignment2 discussion prompts
In this module, we introduce the general definition of angular momentum operator based on rotation operator. This general definition allows both orbital and spin angular momentum. We then derive the most fundamental property of angular momentum - commutation relations among their Cartesian components. Finally, we discuss the properties of spin-1/2 system.
What's included
4 videos3 readings1 assignment1 discussion prompt
This module covers the general theory of angular momentum. We start with the commutation relation of angular momentum and define angular momentum eigenstates. We then construct matrix representation of rotation operators using the angular momentum eigenstates as the basis set. Finally, we discuss how to quantum mechanically add angular momenta.
What's included
6 videos3 readings1 assignment1 peer review
Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV. Share it on social media and in your performance review.
Build toward a degree
This course is part of the following degree program(s) offered by University of Colorado Boulder. If you are admitted and enroll, your completed coursework may count toward your degree learning and your progress can transfer with you.¹
Instructor
Instructor ratings
3.8 (5 ratings)Offered by
Explore more from Electrical Engineering
Status: Free Trial
Status: Free TrialLearnQuest
Status: Free TrialUniversity of Colorado Boulder
Status: Free TrialLearnQuest
Why people choose Coursera for their career
Felipe M.
Learner since 2018
"To be able to take courses at my own pace and rhythm has been an amazing experience. I can learn whenever it fits my schedule and mood."
Jennifer J.
Learner since 2020
"I directly applied the concepts and skills I learned from my courses to an exciting new project at work."
Larry W.
Learner since 2021
"When I need courses on topics that my university doesn't offer, Coursera is one of the best places to go."
Chaitanya A.
"Learning isn't just about being better at your job: it's so much more than that. Coursera allows me to learn without limits."
Learner reviews
4.0
20 reviews
- 5 stars
55%
- 4 stars
20%
- 3 stars
5%
- 2 stars
15%
- 1 star
5%
Showing 3 of 20
GV
5
Reviewed on Jun 16, 2023
Very nice course. Good textbook (Sakurai). Good teaching.
Open new doors with Coursera Plus
Unlimited access to 10,000+ world-class courses, hands-on projects, and job-ready certificate programs - all included in your subscription
Advance your career with an online degree
Earn a degree from world-class universities - 100% online
Join over 3,400 global companies that choose Coursera for Business
Upskill your employees to excel in the digital economy
Frequently asked questions
Access to lectures and assignments depends on your type of enrollment. If you take a course in audit mode, you will be able to see most course materials for free. To access graded assignments and to earn a Certificate, you will need to purchase the Certificate experience, during or after your audit. If you don't see the audit option:
The course may not offer an audit option. You can try a Free Trial instead, or apply for Financial Aid.
The course may offer 'Full Course, No Certificate' instead. This option lets you see all course materials, submit required assessments, and get a final grade. This also means that you will not be able to purchase a Certificate experience.
When you enroll in the course, you get access to all of the courses in the Specialization, and you earn a certificate when you complete the work. Your electronic Certificate will be added to your Accomplishments page - from there, you can print your Certificate or add it to your LinkedIn profile. If you only want to read and view the course content, you can audit the course for free.
If you subscribed, you get a 7-day free trial during which you can cancel at no penalty. After that, we don’t give refunds, but you can cancel your subscription at any time. See our full refund policy.
More questions
Financial aid available,