This course will focus on theory and implementation of hypothesis testing, especially as it relates to applications in data science. Students will learn to use hypothesis tests to make informed decisions from data. Special attention will be given to the general logic of hypothesis testing, error and error rates, power, simulation, and the correct computation and interpretation of p-values. Attention will also be given to the misuse of testing concepts, especially p-values, and the ethical implications of such misuse.

Enjoy unlimited growth with a year of Coursera Plus for $199 (regularly $399). Save now.

Statistical Inference and Hypothesis Testing in Data Science Applications
This course is part of Data Science Foundations: Statistical Inference Specialization

Instructor: Jem Corcoran
7,810 already enrolled
Included with
(50 reviews)
Recommended experience
What you'll learn
Define a composite hypothesis and the level of significance for a test with a composite null hypothesis.
Define a test statistic, level of significance, and the rejection region for a hypothesis test. Give the form of a rejection region.
Perform tests concerning a true population variance.
Compute the sampling distributions for the sample mean and sample minimum of the exponential distribution.
Skills you'll gain
Details to know

Add to your LinkedIn profile
1 quiz, 5 assignments
See how employees at top companies are mastering in-demand skills

Build your subject-matter expertise
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate

There are 6 modules in this course
Welcome to the course! This module contains logistical information to get you started!
What's included
3 readings1 discussion prompt1 ungraded lab
In this module, we will define a hypothesis test and develop the intuition behind designing a test. We will learn the language of hypothesis testing, which includes definitions of a null hypothesis, an alternative hypothesis, and the level of significance of a test. We will walk through a very simple test.
What's included
6 videos11 readings1 quiz1 programming assignment2 ungraded labs
In this module, we will expand the lessons of Module 1 to composite hypotheses for both one and two-tailed tests. We will define the “power function” for a test and discuss its interpretation and how it can lead to the idea of a “uniformly most powerful” test. We will discuss and interpret “p-values” as an alternate approach to hypothesis testing.
What's included
7 videos7 readings1 assignment1 programming assignment1 ungraded lab
In this module, we will learn about the chi-squared and t distributions and their relationships to sampling distributions. We will learn to identify when hypothesis tests based on these distributions are appropriate. We will review the concept of sample variance and derive the “t-test”. Additionally, we will derive our first two-sample test and apply it to make some decisions about real data.
What's included
7 videos7 readings1 assignment1 programming assignment1 ungraded lab
In this module, we will consider some problems where the assumption of an underlying normal distribution is not appropriate and will expand our ability to construct hypothesis tests for this case. We will define the concept of a “uniformly most powerful” (UMP) test, whether or not such a test exists for specific problems, and we will revisit some of our earlier tests from Modules 1 and 2 through the UMP lens. We will also introduce the F-distribution and its role in testing whether or not two population variances are equal.
What's included
6 videos6 readings2 assignments
In this module, we develop a formal approach to hypothesis testing, based on a “likelihood ratio” that can be more generally applied than any of the tests we have discussed so far. We will pay special attention to the large sample properties of the likelihood ratio, especially Wilks’ Theorem, that will allow us to come up with approximate (but easy) tests when we have a large sample size. We will close the course with two chi-squared tests that can be used to test whether the distributional assumptions we have been making throughout this course are valid.
What's included
5 videos5 readings1 assignment1 programming assignment1 ungraded lab
Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV. Share it on social media and in your performance review.
Build toward a degree
This course is part of the following degree program(s) offered by University of Colorado Boulder. If you are admitted and enroll, your completed coursework may count toward your degree learning and your progress can transfer with you.¹
Instructor

Offered by
Explore more from Probability and Statistics

University of Colorado Boulder
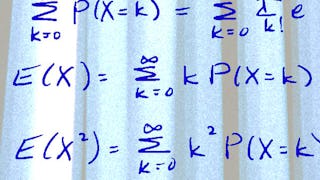 Status: Free Trial
Status: Free TrialUniversity of Colorado Boulder
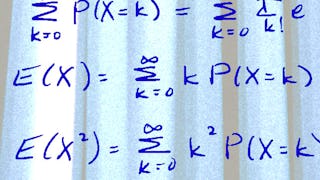 Status: Free Trial
Status: Free TrialUniversity of Colorado Boulder
 Status: Preview
Status: PreviewBall State University
Why people choose Coursera for their career




Learner reviews
50 reviews
- 5 stars
78%
- 4 stars
14%
- 3 stars
4%
- 2 stars
0%
- 1 star
4%
Showing 3 of 50
Reviewed on Feb 8, 2024
Great course, challenging quizzes. Labs and programming assignments are really helpful, especially the one on Wilks theorem, I really liked that one.
Reviewed on Jul 6, 2023
coursera classes can be rough and maybe even a little bit buggy it's loaded with good knowlede tho. the professor is great!
Reviewed on Oct 26, 2022
In-depth course on Hypothesis testing. Course instructor is quite engaging.
Frequently asked questions
To access the course materials, assignments and to earn a Certificate, you will need to purchase the Certificate experience when you enroll in a course. You can try a Free Trial instead, or apply for Financial Aid. The course may offer 'Full Course, No Certificate' instead. This option lets you see all course materials, submit required assessments, and get a final grade. This also means that you will not be able to purchase a Certificate experience.
When you enroll in the course, you get access to all of the courses in the Specialization, and you earn a certificate when you complete the work. Your electronic Certificate will be added to your Accomplishments page - from there, you can print your Certificate or add it to your LinkedIn profile.
Yes. In select learning programs, you can apply for financial aid or a scholarship if you can’t afford the enrollment fee. If fin aid or scholarship is available for your learning program selection, you’ll find a link to apply on the description page.
More questions
Financial aid available,